基本操作
节点
// 节点区间定义
// [start, end] 代表节点的区间范围
// max 是节点在(start,end)区间上的最大值
// left , right 是当前节点区间划分之后的左右节点区间
public class SegmentTreeNode {
public int start, end, max;
public SegmentTreeNode left, right;
public SegmentTreeNode(int start, int end, int max) {
this.start = start;
this.end = end;
this.max = max
this.left = this.right = null;
}
}
线段树区间最大值维护
给定一个区间，我们要维护线段树中存在的区间中最大的值。这将有利于我们高效的查询任何区间的最大值。给出A数组，基于A数组构建一棵维护最大值的线段树，我们可以在O(logN)的复杂度内查询任意区间的最大值：
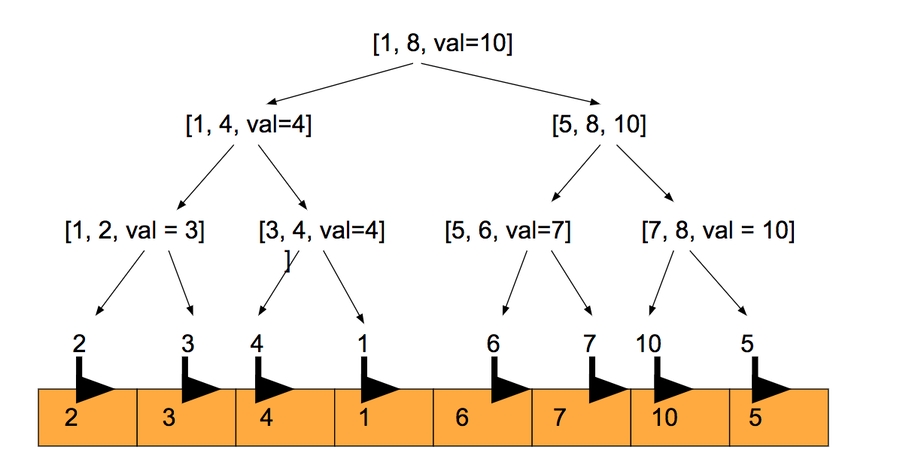
比如原数组A = [1, 4, 2, 3]
[0,3]
(val=4)
/ \
[0,1] [2,3]
(val=4) (val=3)
/ \ / \
[0,0] [1,1] [2,2] [3,3]
(val=1)(val=4) (val=2)(val=3)
// 构造的代码及注释
public SegmentTreeNode build(int[] A) {
// write your code here
return buildhelper(0, A.length - 1, A);
}
线段树的建立
public SegmentTreeNode buildhelper(int left, int right, int[] A){
if(left > right){
return null;
}
SegmentTreeNode root = new SegmentTreeNode(left, right, A[left]); // 根据节点区间的左边界的序列值为节点赋初值
if(left == right){
return root; // 如果左边界和右边界相等,节点左边界的序列值就是线段树节点的接节点值
}
int mid = (left + right) / 2; // 划分当前区间的左右区间
root.left = buildhelper(left, mid, A);
root.right = buildhelper(mid + 1, right, A);
root.max = Math.max(root.left.max, root.right.max); // 根据节点区间的左右区间的节点值得到当前节点的节点值
return root;
}
举一反三：
如果需要区间的最小值:
root.min = Math.min(root.left.min, root.right.min);
如果需要区间的和:
root.sum = root.left.sum + root.right.sum;
线段树的区间查询
1. 如何更好的查询Query
构造线段树的目的就是为了更快的查询。
给定一个区间，要求区间中最大的值。线段树的区间查询操作就是将当前区间分解为较小的子区间,然后由子区间的最大值就可以快速得到需要查询区间的最大值。
[0,3]
(val=4)
/ \
[0,1] [2,3]
(val=4) (val=3)
/ \ / \
[0,0] [1,1] [2,2] [3,3]
(val=1)(val=4) (val=2)(val=3)
query(1,3) = max(query(1,1),query(2,3)) = max(4,3) = 4
上述例子将[1, 3]区间分为了[1, 1]和[2, 3]两个区间,因为[1, 1]和[2, 3]存在于线段树上，所以区间的最大值已经记录好了,所以直接拿来用就可以了。所以拆分区间的目的是划分成为线段树上已经存在的小线段。
2. 如何拆分区间变成线段树上有的小区间：
第一层会查询试图查询[1, 7], 发现区间不存在，然后根据mid位置拆分[1, 4]和[5, 7]
第二层会查询[1, 4],[5, 7], 发现[1, 4]已经存在，返回即可，[5, 7]仍旧需要继续拆分
第三层会查询[5, 6],[7, 7], 发现[5, 6]已经存在，返回即可，[7, 7]仍旧需要继续拆分
第四层会查询[7, 7]
任意长度的线段，最多被拆分成logn条线段树上存在的线段，所以查询的时间复杂度为O(log(n))记住就好：）
// 区间查询的代码及注释
public int query(TreeNode root, int start, int end) {
if (start <= root.start && root.end <= end) {
// 如果查询区间在当前节点的区间之内,直接输出结果
return root.max;
}
int mid = (root.start + root.end) / 2; // 将当前节点区间分割为左右2个区间的分割线
int ans = Integer.MIN_VALUE; // 给结果赋初值
if (mid >= start) { // 如果查询区间和左边节点区间有交集,则寻找查询区间在左边区间上的最大值
ans = Math.max(ans, query(root.left, start, end));
}
if (mid + 1 <= end) { // 如果查询区间和右边节点区间有交集,则寻找查询区间在右边区间上的最大值
ans = Math.max(ans, query(root.right, start, end));
}
return ans; // 返回查询结果
}
线段树的单点更新
1. 更新序列中的一个点
[0,3]
(val=4)
/ \
[0,1] [2,3]
(val=4) (val=3)
/ \ / \
[0,0] [1,1] [2,2] [3,3]
(val=1)(val=4) (val=2)(val=3)
更新序列中的一个节点，如何把这种变化体现到线段树中去，例如，将序列中的第4个点A[3]更新为5, 要变动3个区间中的值,分别为[3,3],[2,3],[0,3]
提问：为什么需要更新这三个区间？：因为只有这三个在线段树中的区间，覆盖了3这个点。
[0,3]
(val=5)
/ \
[0,1] [2,3]
(val=4) (val=5)
/ \ / \
[0,0] [1,1] [2,2] [3,3]
(val=1)(val=4) (val=2)(val=5)
可以这样想,改动一个节点,与这个节点对应的叶子节点需要变动。因为叶子节点的值的改变可能影响到父亲节点，然后叶子节点的父亲节点也可能需要变动。
如果我们继续把A[2]从2变成4，线段树又该如何更新呢？
线段树变化后的状态为：
[0,3]
(val=5)
/ \
[0,1] [2,3]
(val=4) (val=5)
/ \ / \
[0,0] [1,1] [2,2] [3,3]
(val=1)(val=4) (val=4)(val=5)
如果我们继续把A[1]从4变成3，线段树又该如何更新呢？
线段树变化后的状态为：
[0,3]
(val=5)
/ \
[0,1] [2,3]
(val=3) (val=5)
/ \ / \
[0,0] [1,1] [2,2] [3,3]
(val=1)(val=3) (val=4)(val=5)
更新所以需要从叶子节点一路走到根节点, 去更新线段树上的值。因为线段树的高度为log(n),所以更新序列中一个节点的复杂度为log(n)。
因为每次从父节点走到子节点的时候，区间都是一分为二，那么我们要修改index的时候，我们从root出发，判断index会落在左边还是右边，然后继续递归，这样就可以很容易从根节点走到叶子节点，然后更新叶子节点的值，递归返回前不断更新每个节点的最大值即可。具体代码实现如下：
// 单点更新的代码及注释
public void modify(SegmentTreeNode root, int index, int value) {
// write your code here
if(root.start == root.end && root.start == index) { // 找到被改动的叶子节点
root.max = value; // 改变value值
return ;
}
int mid = (root.start + root.end) / 2; // 将当前节点区间分割为2个区间的分割线
if(index <= mid){ // 如果index在当前节点的左边
modify(root.left, index, value); // 递归操作
root.max = Math.max(root.right.max, root.left.max); // 可能对当前节点的影响
}
else { // 如果index在当前节点的右边
modify(root.right, index, value); // 递归操作
root.max = Math.max(root.left.max, root.right.max); // 可能对当前节点的影响
}
return ;
}
如果需要区间的最小值或者区间的和，构造的时候同理。
总结
通过前面问题的分析，我们对线段树问题可以做如下总结：
1 如果问题带有区间操作，或者可以转化成区间操作，可以尝试往线段树方向考虑
从面试官给的题目中抽象问题，将问题转化成一列区间操作，注意这步很关键
2 当我们分析出问题是一些列区间操作的时候
我们都可以采用线段树来解决这个问题
3 套用我们前面讲到的经典步骤和写法，即可在面试中完美的解决这些题目！
什么情况下，无法使用线段树？
如果我们删除或者增加区间中的元素，那么区间的大小将发生变化，此时是无法使用线段树解决这种问题的。
