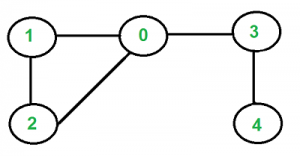
Detect Cycle in an Undirected Graph

Given an undirected graph, how to check if there is a cycle in the graph? For example, the following graph has a cycle 1-0-2-1.

Like directed graphs, we can use DFS to detect cycle in an undirected graph in O(V+E) time. We do a DFS traversal of the given graph. For every visited vertex ‘v’, if there is an adjacent ‘u’ such that u is already visited and u is not parent of v, then there is a cycle in graph. If we don’t find such an adjacent for any vertex, we say that there is no cycle. The assumption of this approach is that there are no parallel edges between any two vertices.

// A Java Program to detect cycle in an undirected graph
import java.io.*;
import java.util.*;

// This class represents a directed graph using adjacency list
// representation
class Graph
{
    private int V;   // No. of vertices
    private LinkedList<Integer> adj[]; // Adjacency List Represntation

    // Constructor
    Graph(int v) {
        V = v;
        adj = new LinkedList[v];
        for(int i=0; i<v; ++i)
            adj[i] = new LinkedList();
    }

    // Function to add an edge into the graph
    void addEdge(int v,int w) {
        adj[v].add(w);
        adj[w].add(v);
    }

    // A recursive function that uses visited[] and parent to detect
    // cycle in subgraph reachable from vertex v.
    Boolean isCyclicUtil(int v, Boolean visited[], int parent)
    {
        // Mark the current node as visited
        visited[v] = true;
        Integer i;

        // Recur for all the vertices adjacent to this vertex
        Iterator<Integer> it = adj[v].iterator();
        while (it.hasNext())
        {
            i = it.next();

            // If an adjacent is not visited, then recur for that
            // adjacent
            if (!visited[i])
            {
                if (isCyclicUtil(i, visited, v))
                    return true;
            }

            // If an adjacent is visited and not parent of current
            // vertex, then there is a cycle.
            else if (i != parent)
                return true;
        }
        return false;
    }

    // Returns true if the graph contains a cycle, else false.
    Boolean isCyclic()
    {
        // Mark all the vertices as not visited and not part of
        // recursion stack
        Boolean visited[] = new Boolean[V];
        for (int i = 0; i < V; i++)
            visited[i] = false;

        // Call the recursive helper function to detect cycle in
        // different DFS trees
        for (int u = 0; u < V; u++)
            if (!visited[u]) // Don't recur for u if already visited
                if (isCyclicUtil(u, visited, -1))
                    return true;

        return false;
    }

    // Driver method to test above methods
    public static void main(String args[])
    {
        // Create a graph given in the above diagram
        Graph g1 = new Graph(5);
        g1.addEdge(1, 0);
        g1.addEdge(0, 2);
        g1.addEdge(2, 0);
        g1.addEdge(0, 3);
        g1.addEdge(3, 4);
        if (g1.isCyclic())
            System.out.println("Graph contains cycle");
        else
            System.out.println("Graph doesn't contains cycle");

        Graph g2 = new Graph(3);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        if (g2.isCyclic())
            System.out.println("Graph contains cycle");
        else
            System.out.println("Graph doesn't contains cycle");
    }
}

We do a BFS traversal of the given graph. For every visited vertex ‘v’, if there is an adjacent ‘u’ such that u is already visited and u is not parent of v, then there is a cycle in graph. If we don’t find such an adjacent for any vertex, we say that there is no cycle. The assumption of this approach is that there are no parallel edges between any two vertices.

We use a parent array to keep track of parent vertex for a vertex so that we do not consider visited parent as cycle.

boolean isCyclicConntected(vector<int> adj[], int s,
                           int V, vector<bool>& visited)
{
    // Set parent vertex for every vertex as -1.
    vector<int> parent(V, -1);

    // Create a queue for BFS
    queue<int> q;

    // Mark the current node as visited and enqueue it
    visited[s] = true;
    q.push(s);

    while (!q.empty()) {

        // Dequeue a vertex from queue and print it
        int u = q.front();
        q.pop();

        // Get all adjacent vertices of the dequeued
        // vertex s. If a adjacent has not been visited,
        // then mark it visited and enqueue it. We also
        // mark parent so that parent is not considered
        // for cycle.
        for (auto v : adj[u]) {
            if (!visited[v]) {
                visited[v] = true;
                q.push(v);
                parent[v] = u;
            }
            else if (parent[u] != v)
                return true;
        }
    }
    return false;
}

bool isCyclicDisconntected(vector<int> adj[], int V)
{
    // Mark all the vertices as not visited
    vector<bool> visited(V, false);

    for (int i = 0; i < V; i++)
        if (!visited[i] && isCyclicConntected(adj, i, V, visited))
            return true;
    return false;
}