0 Binary Search Tree
定义
二叉搜索树（Binary Search Tree，又名排序二叉树，二叉查找树，通常简写为BST）定义如下：
空树或是具有下列性质的二叉树：
（1）若左子树不空，则左子树上所有节点值均小于或等于它的根节点值；
（2）若右子树不空，则右子树上所有节点值均大于或等于它的根节点值；
（3）左、右子树也为二叉搜索树；
如图即为BST：
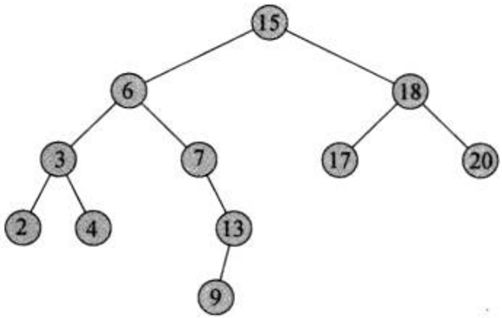
BST 的特性
按照中序遍历（inorder traversal）打印各节点，会得到由小到大的顺序。
在BST中搜索某值的平均时间复杂度为O(logN)，其中N为节点个数。类似二分查找（binary search），将待寻值与节点值比较，若不相等，则通过是小于还是大于，可断定该值只可能在左子树还是右子树，继续向该子树搜索。故一次比较平均排除半棵树。
BST 的作用
通过中序遍历，可快速得到升序节点列表。
在BST中查找元素，只需要平均O(logN)的时间，这与有序数组（sorted array）一样。但BST平均log(N)即可实现元素的增加和删除（参考链接），有序数组却需要O(N)
二叉搜索树(Binary Search Tree)的CRUD操作
二叉搜索树可以是一棵空树或者是一棵满足下列条件的二叉树:
如果它的左子树不空，则左子树上所有节点值
均小于它的根节点值。
如果它的右子树不空，则右子树上所有节点值
均大于它的根节点值。
它的左右子树均为二叉搜索树(BST)。
严格定义下BST中是没有值相等的节点的(No duplicate nodes)。
根据上述特性，我们可以得到一个结论：BST中序遍历得到的序列是升序的。如下述BST的中序序列为：[1,3,4,6,7,8,10,13,14]
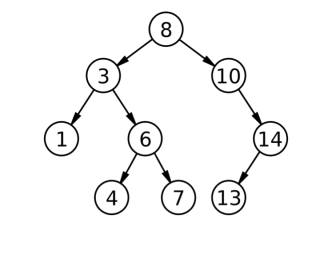
BST基本操作——增删改查(CRUD)
对于树节点的定义如下：
class TreeNode{
int val;
TreeNode left;
TreeNode right;
pubic TreeNode(int val) {
this.val = val;
this.left = this.right = null;
}
}基本操作之查找(Retrieve)
思路
查找值为val的节点，如果val小于根节点则在左子树中查找，反之在右子树中查找
代码实现
public TreeNode searchBST(TreeNode root, int val) {
if (root == null) {
return null;
}// 未找到值为val的节点
if (val < root.val) {
return searchBST(root.left, val);//val小于根节点值，在左子树中查找
} else if (val > root.val) {
return searchBST(root.right, val);//val大于根节点值，在右子树中查找
} else {
return root;//找到了
}
}实战
基本操作之修改(Update)
思路
修改仅仅需要在查找到需要修改的节点之后，更新这个节点的值就可以了
代码实现
public void updateBST(TreeNode root, int target, int val) {
if (root == null) {
return;
}// 未找到target节点
if (target < root.val) {
updateBST(root.left, target, val);//target小于根节点值，在左子树中查找
} else if (target > root.val) {
updateBST(root.right, target, val);//target大于根节点值，在右子树中查找
} else { //找到了
root.val = val;
}
}基本操作之增加(Create)
思路
根节点为空，则待添加的节点为根节点
如果待添加的节点值小于根节点，则在左子树中添加
如果待添加的节点值大于根节点，则在右子树中添加
我们统一在树的叶子节点(Leaf Node)后添加
代码实现
public TreeNode insertNode(TreeNode root, TreeNode node) {
if (root == null) {
return node;
}
if (root.val > node.val) {
root.left = insertNode(root.left, node);
} else {
root.right = insertNode(root.right, node);
}
return root;
}基本操作之删除(Delete)
思路(最为复杂)
考虑待删除的节点为叶子节点，可以直接删除并修改父亲节点(Parent Node)的指针，需要区分待删节点是否为根节点
考虑待删除的节点为单支节点(只有一棵子树——左子树 or 右子树)，与删除链表节点操作类似，同样的需要区分待删节点是否为根节点
考虑待删节点有两棵子树，可以将待删节点与左子树中的最大节点进行交换，由于左子树中的最大节点一定为叶子节点，所以这时再删除待删的节点可以参考第一条
代码实现
public TreeNode removeNode(TreeNode root, int value) {
TreeNode dummy = new TreeNode(0);
dummy.left = root;
TreeNode parent = findNode(dummy, root, value);
TreeNode node;
if (parent.left != null && parent.left.val == value) {
node = parent.left;
} else if (parent.right != null && parent.right.val == value) {
node = parent.right;
} else {
return dummy.left;
}
deleteNode(parent, node);
return dummy.left;
}
private TreeNode findNode(TreeNode parent, TreeNode node, int value) {
if (node == null) {
return parent;
}
if (node.val == value) {
return parent;
}
if (value < node.val) {
return findNode(node, node.left, value);
} else {
return findNode(node, node.right, value);
}
}
private void deleteNode(TreeNode parent, TreeNode node) {
if (node.right == null) {
if (parent.left == node) {
parent.left = node.left;
} else {
parent.right = node.left;
}
} else {
TreeNode temp = node.right;
TreeNode father = node;
while (temp.left != null) {
father = temp;
temp = temp.left;
}
if (father.left == temp) {
father.left = temp.right;
} else {
father.right = temp.right;
}
if (parent.left == node) {
parent.left = temp;
} else {
parent.right = temp;
}
temp.left = node.left;
temp.right = node.right;
}
}常见的BST面试题
http://www.lintcode.com/en/tag/binary-search-tree/
BST是一种重要且基本的结构，其相关题目也十分经典，并延伸出很多算法。 在BST之上，有许多高级且有趣的变种,以解决各式各样的问题，例如:
Last updated